Tree : 나무를 뒤집어 놓은 듯한 모습으로, 여러 구조 중 단방향 그래프이며 하나의 뿌리로부터 가지가 사방으로 뻗은 형태의 자료구조
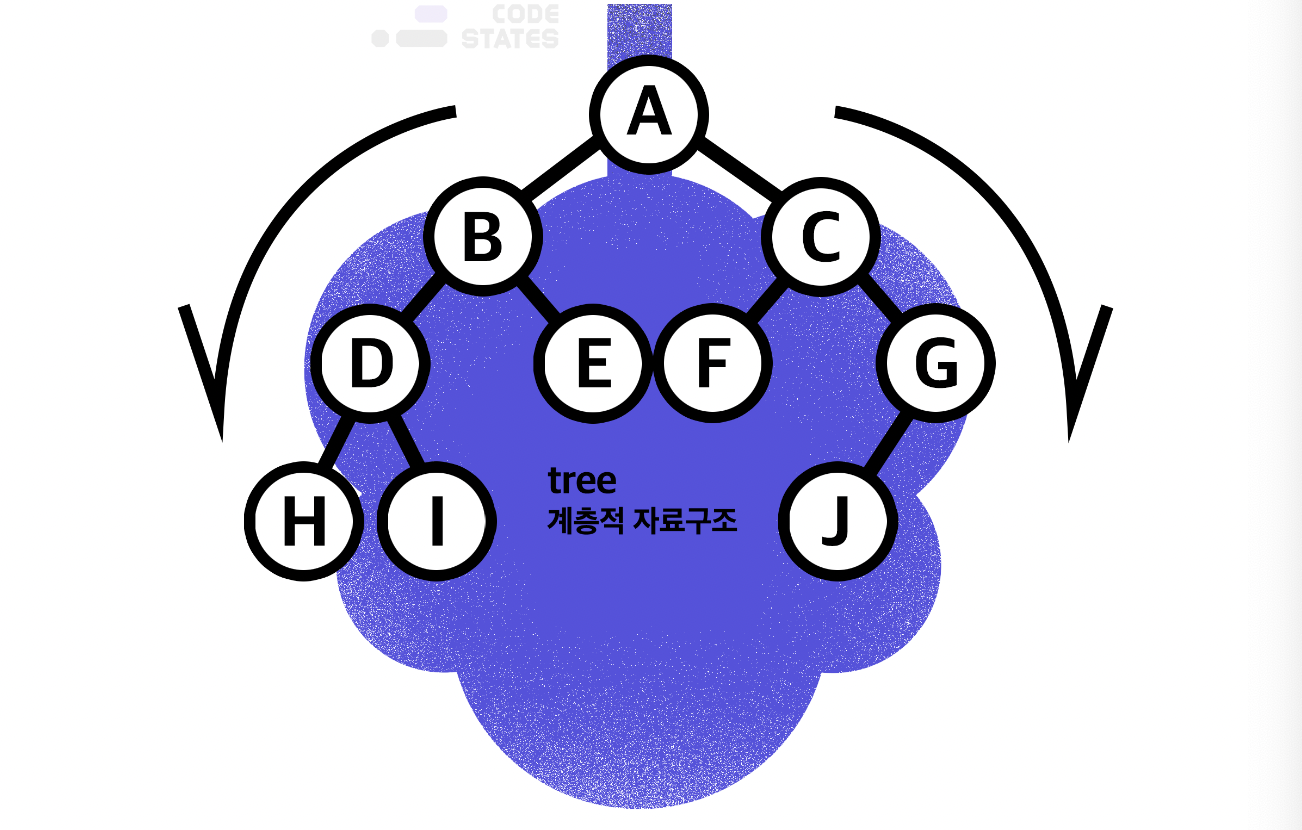
- 하나 이상의 데이터에 한 개의 경로와 하나의 방향으로만 연결된 계층적 자료구조(비선형구조)
트리는 계층적으로 표현되고, 아래로만 뻗어나가기 때문에 사이클이 없다.
(사이클: 시작 노드에서 출발해 다른 노드를 거쳐 시작 노드로 돌아오는 것.)
[Tree 구조와 특징]

- 제일 위 시작점 A : Root(루트)
- 하나의 꼭짓점 데이터를 시작으로 데이터의 연결 선 : Edge(간선)
- 각 데이터들 : Node(노드) >> 노드는 상하 계층으로 연결되어 상(부모 노드), 하(자식 노드)를 형성한다.
>> 자식이 없는 노드 : Leaf Node(리프노드)
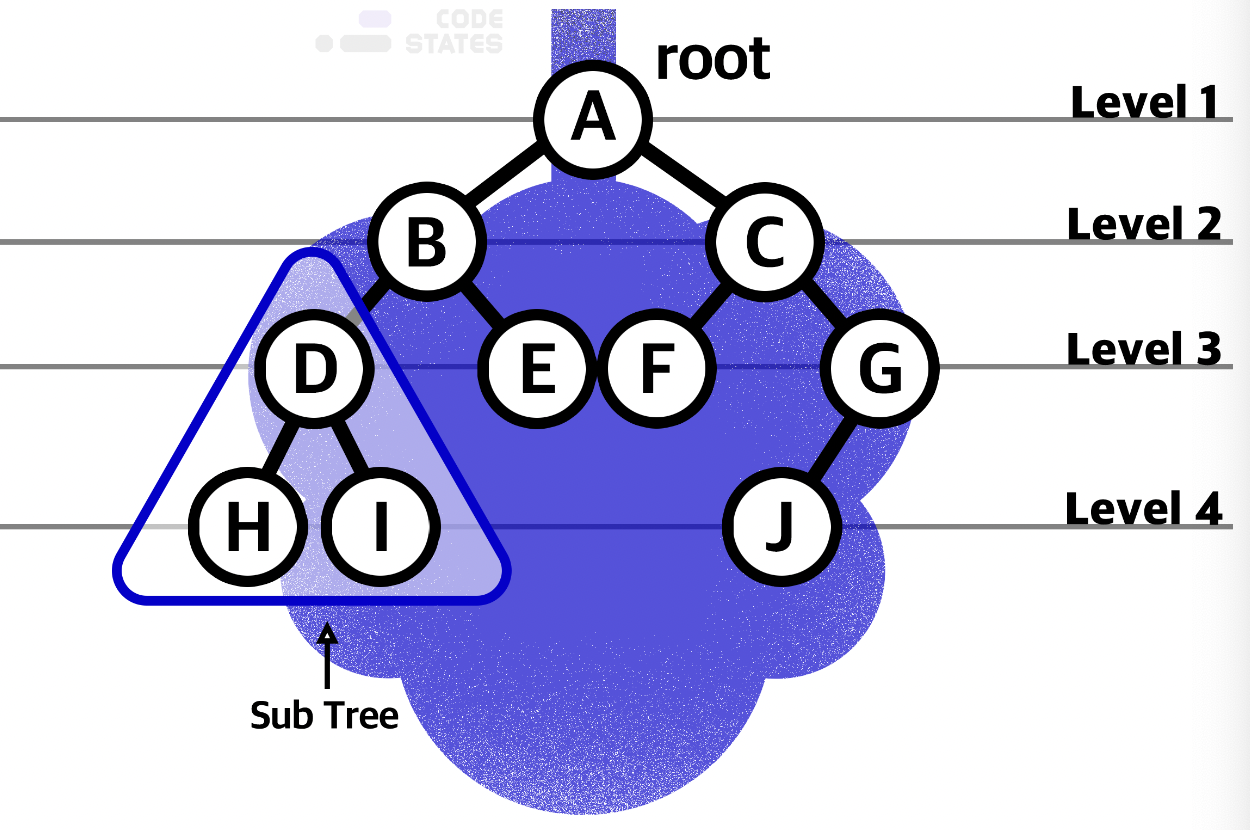
- depth(깊이): 루트로부터 그 아래의 특정 노드까지의 깊이를 표현할 수 있다. 루트 노드 A 가 깊이 0 , 선이 뻗어질 수록 깊이가 생긴다.
>> A: 0 depth, B,C : 1 depth, D,E,F,G : 2depth, H,I,J : 3depth
- level(레벨): 같은 깊이를 가지고 있는 노드를 묶어서 레벨로 표현할 수 있다. 깊이가 0 >> level 1, 깊이가 1 >> level 2...
같은 레벨에 나란히 있는 노드 : 형제 노드(Sibiling Node)
-Height(높이): 리프노드(자식이 없는 노드)를 기준으로 루트까지의 높이를 표현한다.
>> 자식이 없으면 높이 0 , 자식이 있으면 1, 자식의 자식이 있으면 2...
- Sub tree(서브 트리): 트리 구조의 루트에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 서브 트리라고 부른다.
[Tree의 실사용] - 컴퓨터의 디렉토리 구조

+) 월드컵 토너먼트 대진표, 가계도(족보), 조직도 등
[이진트리 Binary Tree]
자식 노드가 최대 두 개인 노드로 구성된 트리 (왼쪽 자식 노드 / 오른쪽 자식 노드)
자료의 삽입, 삭제 방법에 따라 세 가지의 트리로 나뉜다.

- 정 이진 트리(Full binary tree): 각 노드가 0개 혹은 2개의 자식 노드를 갖는다 >> 1개 X
- 포화 이진 트리(Perfect binary tree): 정 이진 트리 && 완전 이진트리 : 모든 레벨이 가득 채워져 있는 트리
- 완전 이진 트리(Complete binary tree): 마지막 레벨을 제외한 노드가 채워져 있어야 하며, 노드의 자식은 왼쪽부터 채운다.
[이진 탐색 트리 Binary Search Tree] : 이진 탐색 + 이진 트리
이진 탐색 : 정렬된 데이터 중에서 특정한 값을 찾기 위한 탐색 알고리즘.
오름차순으로 정렬된 정수의 배열을 같은 크기의 두 부분의 배열로 나누고,
두 부분 중 탐색이 필요한 부분만 택하여 탐색하는 과정을 반복하여, 원하는 값을 찾는 알고리즘.

루트인 10이 이진탐색의 배열의 첫 중간값이 되고,
각 노드의 왼쪽 자식은 노드 보다 작은 값,
각 노드의 오른쪽 자식은 노드보다 큰 값을 가진다.
>> 균형 잡힌 트리가 아니라면, 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰릴 수 있다
ex) 10, 11, 14, 16, 18 순서로 들어온다면 오른쪽으로만 기우는 트리가 된다.
따라서 이 문제를 해결하기 위해 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가하기도 한다,
[이진 탐색 트리의 특징]
기존 이진 트리보다 탐색이 빠르다. >> 복잡도 O(n), 평균 O(log2n)
- 루트 노드의 키와 찾고자 하는 값을 비교합니다. 만약 찾고자 하는 값이라면 탐색을 종료합니다.
- 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행합니다.
- 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행합니다.
위의 과정을 트리의 높이 만큼 반복한다.
+) 찾고자 하는 값이 없더라도 최대 트리의 높이 만큼 탐색이 진행

'TIL' 카테고리의 다른 글
| AWS (0) | 2023.03.31 |
|---|---|
| 자료구조(트리 순회) (0) | 2023.03.15 |
| 웹 표준 & 웹 접근성 (0) | 2023.03.01 |
| CDD (0) | 2023.02.21 |
| Figma (마이리얼트립 clone) (0) | 2023.02.17 |


